Цифровые схемы — мультиплексоры
Мультиплексор — это комбинационная схема, которая имеет максимум 2 n входов данных, n линий выбора и одну выходную линию. Один из этих входов данных будет подключен к выходу на основе значений линий выбора.
Так как есть n строк выбора, будет 2 n возможных комбинаций нулей и единиц. Итак, каждая комбинация выберет только один ввод данных. Мультиплексор также называется Mux .
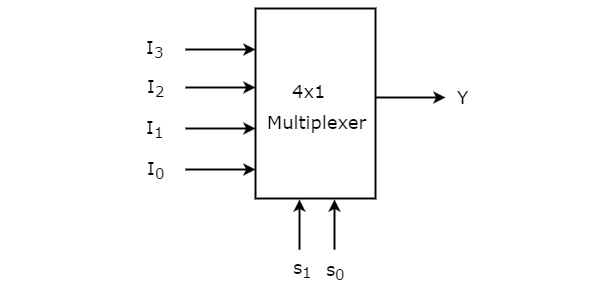
4×1 Мультиплексор
Мультиплексор 4×1 имеет четыре входа данных I 3 , I 2 , I 1 и I 0 , две строки выбора s 1 & s 0 и один выход Y. Блок-схема мультиплексора 4×1 показана на следующем рисунке.
Один из этих 4 входов будет подключен к выходу на основе комбинации входов, присутствующих в этих двух линиях выбора. Таблица истинности мультиплексора 4×1 показана ниже.
| Линии выбора | Выход | |
|---|---|---|
| S 1 | S 0 | Y |
| 0 | 0 | Я 0 |
| 0 | 1 | Я 1 |
| 1 | 0 | Я 2 |
| 1 | 1 | Я 3 |
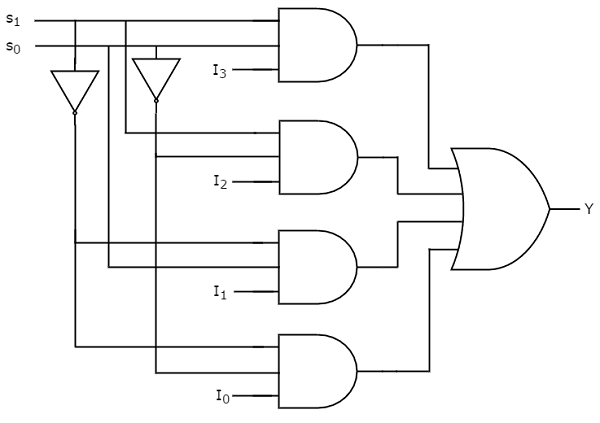
Из таблицы Truth мы можем напрямую написать булеву функцию для вывода, Y как
Y = S 1 ′ S 0 ′ I 0 + S 1 ′ S 0 I 1 + S 1 S 0 ′ I 2 + S 1 S 0 I 3
Мы можем реализовать эту булеву функцию с помощью инверторов, вентилей AND и вентиля OR. Принципиальная схема мультиплексора 4×1 показана на следующем рисунке.
Мы можем легко понять работу вышеупомянутой схемы. Аналогично, вы можете реализовать мультиплексор 8×1 и мультиплексор 16×1, следуя той же процедуре.
Реализация мультиплексоров высшего порядка.
Теперь давайте реализуем следующие два мультиплексора высшего порядка, используя мультиплексоры низкого порядка.
- 8×1 мультиплексор
- 16×1 мультиплексор
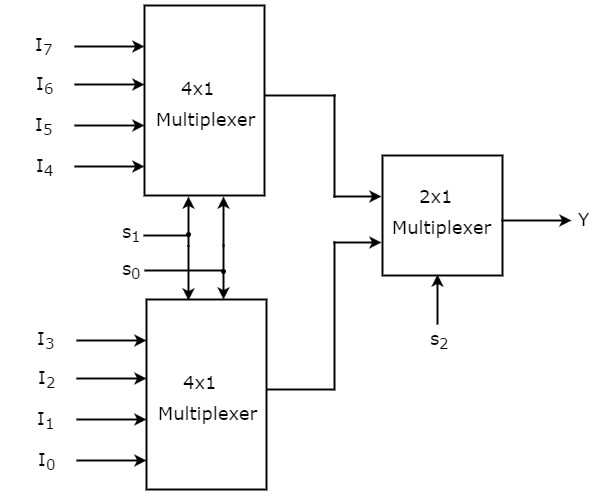
8×1 мультиплексор
В этом разделе мы реализуем мультиплексор 8×1, используя мультиплексоры 4×1 и мультиплексор 2×1. Мы знаем, что 4×1 Multiplexer имеет 4 входа данных, 2 строки выбора и один выход. Принимая во внимание, что мультиплексор 8×1 имеет 8 входов данных, 3 строки выбора и один выход.
Итак, нам требуется два мультиплексора 4×1 на первом этапе, чтобы получить 8 входных данных. Поскольку каждый мультиплексор 4×1 производит один выходной сигнал, нам требуется мультиплексор 2×1 на втором этапе, рассматривая выходы первого этапа в качестве входных данных и для получения конечного выхода.
Пусть мультиплексор 8×1 имеет восемь входов данных от I 7 до I 0 , три строки выбора s 2 , s 1 & s0 и один выход Y. Таблица истинности мультиплексора 8×1 показана ниже.
| Выбор входов | Выход | ||
|---|---|---|---|
| S 2 | S 1 | S 0 | Y |
| 0 | 0 | 0 | Я 0 |
| 0 | 0 | 1 | Я 1 |
| 0 | 1 | 0 | Я 2 |
| 0 | 1 | 1 | Я 3 |
| 1 | 0 | 0 | Я 4 |
| 1 | 0 | 1 | Я 5 |
| 1 | 1 | 0 | Я 6 |
| 1 | 1 | 1 | Я 7 |
Мы можем легко реализовать мультиплексор 8×1, используя мультиплексоры низкого порядка, рассмотрев приведенную выше таблицу истинности. Блок-схема мультиплексора 8×1 показана на следующем рисунке.
Те же строки выбора, s 1 и s 0 , применяются к обоим мультиплексорам 4×1. Входы данных верхнего мультиплексора 4×1 — от I 7 до I 4, а входы данных нижнего мультиплексора 4×1 — от I 3 до I 0 . Таким образом, каждый мультиплексор 4×1 создает выходной сигнал на основе значений строк выбора, s 1 и s 0 .
Выходы мультиплексоров 4×1 первой ступени применяются в качестве входов мультиплексора 2×1, который присутствует на второй ступени. Другая строка выбора s 2 применяется к мультиплексору 2×1.
Если s 2 равно нулю, то выход мультиплексора 2×1 будет одним из 4 входов от I 3 до I 0 на основе значений линий выбора s 1 & s 0 .
Если s 2 равно единице, то выход мультиплексора 2×1 будет одним из 4 входов от I 7 до I 4 на основе значений линий выбора s 1 & s 0 .
Если s 2 равно нулю, то выход мультиплексора 2×1 будет одним из 4 входов от I 3 до I 0 на основе значений линий выбора s 1 & s 0 .
Если s 2 равно единице, то выход мультиплексора 2×1 будет одним из 4 входов от I 7 до I 4 на основе значений линий выбора s 1 & s 0 .
Таким образом, общая комбинация двух мультиплексоров 4×1 и одного мультиплексора 2×1 работает как один мультиплексор 8×1.
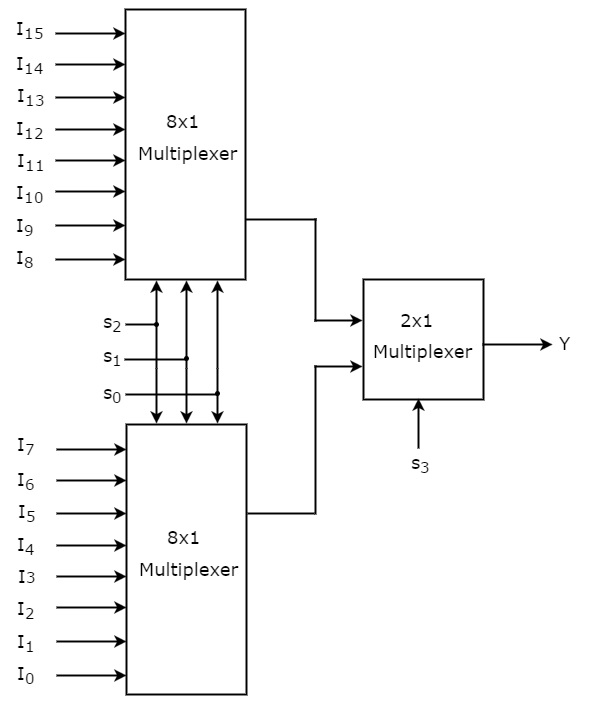
16×1 мультиплексор
В этом разделе мы реализуем мультиплексор 16×1, используя мультиплексоры 8×1 и мультиплексор 2×1. Мы знаем, что мультиплексор 8×1 имеет 8 входов данных, 3 строки выбора и один выход. Принимая во внимание, что мультиплексор 16×1 имеет 16 входов данных, 4 строки выбора и один выход.
Итак, нам требуется два мультиплексора 8×1 на первом этапе, чтобы получить 16 входных данных. Так как каждый мультиплексор 8×1 производит один выход, нам требуется мультиплексор 2×1 на втором этапе, рассматривая выходы первого этапа в качестве входных данных и для получения конечного выхода.
Пусть мультиплексор 16×1 имеет шестнадцать входов данных от I 15 до I 0 , четыре строки выбора от s 3 до s 0 и один выход Y. Таблица истинности мультиплексора 16×1 показана ниже.
| Выбор входов | Выход | |||
|---|---|---|---|---|
| S 3 | S 2 | S 1 | S 0 | Y |
| 0 | 0 | 0 | 0 | Я 0 |
| 0 | 0 | 0 | 1 | Я 1 |
| 0 | 0 | 1 | 0 | Я 2 |
| 0 | 0 | 1 | 1 | Я 3 |
| 0 | 1 | 0 | 0 | Я 4 |
| 0 | 1 | 0 | 1 | Я 5 |
| 0 | 1 | 1 | 0 | Я 6 |
| 0 | 1 | 1 | 1 | Я 7 |
| 1 | 0 | 0 | 0 | Мне 8 |
| 1 | 0 | 0 | 1 | Мне 9 |
| 1 | 0 | 1 | 0 | Мне 10 |
| 1 | 0 | 1 | 1 | Мне 11 |
| 1 | 1 | 0 | 0 | Мне 12 |
| 1 | 1 | 0 | 1 | Мне 13 |
| 1 | 1 | 1 | 0 | Мне 14 |
| 1 | 1 | 1 | 1 | Мне 15 |
Мы можем легко реализовать мультиплексор 16×1, используя мультиплексоры низкого порядка, рассмотрев приведенную выше таблицу истинности. Блок-схема мультиплексора 16×1 показана на следующем рисунке.
Те же строки выбора, s 2 , s 1 и s 0 , применяются к обоим мультиплексорам 8×1. Входы данных верхнего мультиплексора 8×1 — от I 15 до I 8, а входы данных нижнего мультиплексора 8×1 — от I 7 до I 0 . Следовательно, каждый мультиплексор 8×1 создает выходной сигнал на основе значений строк выбора, s 2 , s 1 & s 0 .
Выходы мультиплексоров 8×1 первой ступени применяются в качестве входов мультиплексора 2×1, который присутствует на второй ступени. Другая строка выбора s 3 применяется к мультиплексору 2×1.
Если s 3 равно нулю, то выход мультиплексора 2×1 будет одним из 8 входов от 7 до I 0 на основе значений линий выбора s 2 , s 1 & s 0 .
Если s 3 равен единице, то выход мультиплексора 2×1 будет одним из 8 входов от I 15 до I 8 на основании значений линий выбора s 2 , s 1 & s 0 .
Если s 3 равно нулю, то выход мультиплексора 2×1 будет одним из 8 входов от 7 до I 0 на основе значений линий выбора s 2 , s 1 & s 0 .
Если s 3 равен единице, то выход мультиплексора 2×1 будет одним из 8 входов от I 15 до I 8 на основании значений линий выбора s 2 , s 1 & s 0 .
Таким образом, общая комбинация двух мультиплексоров 8×1 и одного мультиплексора 2×1 работает как один мультиплексор 16×1.
Источник
Мультиплексоры. Реализация логических функций на мультиплексорах, страница 2
На основании табл. 3.6 разработано устройство на MUX(2-1), рис. 3.5:
Рис. 3.5 Подключение мультиплексора: а – микросхема, б – механический аналог на переключателе для реализации логической функции
Схему также можно упростить, т.к. наборы 2, 3 (табл. 3.5) можно объединить, подав на А 0: A 1=0, при этом F = X 0 =0 (константа 0); на наборах 4, 5: A 1=1, а значение функции F повторяет значения A 0, которое подается на X 1 (табл. 3.7, рис. 3.6).
Таблица истинности устройства Таблица 3.7
На основании табл. 3.6 разработано устройство на MUX(2-1), рис. 3.5:
Рис. 3.6 Подключение мультиплексора: а – микросхема, б – механический аналог на переключателе для реализации логической функции
Реализация БФ с уменьшением количества информационных входов
Пример. Задана функция, составляется ее таблица истинности:
Таблица истинности Таблица 3.8
Составляем карту Карно и два горизонтально расположенных входных информационных сигналов D 1, D 2 используем для подачи на адресные входы A 0, A 1. Оставшийся информационный сигнал D 0 будем использовать для подачи на информационные входы MUX.
Из карты Карно следует, что при всех значениях D 0 для D 1, D 2 равных 0, 0 (подключен информационный вход D 0) на выходе 1. Аналогичные соображения для других комбинаций D 1, D 2.
Карта Карно Таблица 3.9
Из таблицы 3.9 следует, что значения D 2 D 1: 00 – константа 1; 01 – константа 0;10 – инверсия D 0; 11 – D 0. Эти значения представлены в таблице 3.10.
Таблица истинности Таблица 3.10
D 0‘ – инверсное значение D 0
На рис. 3.7 представлена реализация БФ трех переменных с помощью MUX(4 – 1) согласно таблице 3.10. Если бы не минимизация, то потребовался бы MUX(8 – 1).
Рис. 3.7 Реализация БФ трех переменных с помощью MUX(4 – 1)
Увеличение разрядности мультиплексора
Используя два мультиплексора, например, MUX(2-1) количество входов можно увеличить в два раза, реализуя MUX(4-1), если подавать на входы EI старший разряд адресной переменной ( A 1) со своими значениями, заданными в функции. Этот сигнал будет попеременно подключать в работу первый или второй мультиплексор (рис. 3.6, а; табл. 3.7).
Рис. 3.7 Увеличение разрядности, а – реализация MUX(4-1) на двух MUX(2-1),
б – реализация MUX(3-1) на двух MUX(2-1)
Таблица истинности MUX(4-1) Таблица 3.7
Аналитическое выражение работы MUX(4-1), согласно таблице 3.7 и схеме рис. 3.7, а:
Также увеличение разрядности мультиплексоров можно осуществить за счет их пирамидального включения (рис.3.8).
Из таблицы 3.3 следует, что четным номерам информационных входов X соответствует значение адреса A 0 = 0 и эти входы подключены к MUX 1. Для нечетных номеров информационных входов X адрес A 0 = 1 и эти входы подключены к MUX 2. Младший адресный разряд A 0 используется для управления мультиплексором MUX 3.
В результате из двух мультиплексоров MUX(4-1) и одного MUX(2-1) получился MUX(8-1). Недостаток схемы – снижение быстродействия за счет последовательного включения микросхем. В результате время переключения составит сумму интервалов переключений MUX 1 ( MUX 2) и MUX 3.
Рис. 3.8 Пирамидальное включение мультиплексоров для увеличения разрядности
Аналитическое выражение, соответствующее схеме MUX(8-1), рис. 3.8, если EI = 1:
Данное выражение можно получить из таблицы истинности 3.3 согласно стандартной процедуре.
Достоинство пирамидальной схемы – использование однотипных элементов.
Мультиплексоры также используются для одновременного подключения n— разрядных слов в соответствии с адресом на n— разрядный выход в параллельном коде.
Одновременно к n выходам подключаются n входов. При изменении значения адреса к n выходам одновременно подключаются другие n входов. Мультиплексор обозначается MUX( k – n в n), где k — количество слов.
Например, MUX(4 – 8 в 8) – четыре восьмибитовых слов выборочно передаются на восьмибитовый выход согласно двухразрядному адресному двоичному коду. Применяется в микропроцессорной технике.
Мультиплексоры используются в составе больших интегральных микросхем, например, микропроцессоров, где к одному выходу подключается несколько внутренних источников сигналов. Это позволяет уменьшить размеры микросхем за счет снижения числа выходов, и, следовательно, повысить их быстродействие. В микропроцессорах с одних выходов могут передаваться сигналы линий шины данных и шины адреса, передаваемые последовательно во времени, например, с помощью MUX(4 – 8 в 8).
Примеры использования мультиплексоров:
— передача данных от нескольких источников сигналов по общему каналу с разделением во времени;
— преобразование параллельного кода в последовательный код (модем);
— постоянные запоминающие устройства;
— в качестве дешифраторов;
— регистры сдвига (совместно с приоритетным шифратором);
— преобразование целых чисел из формата с фиксированной запятой в формат с плавающей запятой и обратное преобразование;
— для передачи четырех восьмибитовых слов в параллельном коде на восьмибитовый выход. Применяется в микропроцессорной технике.
Источник
Реализация логических функций на мультиплексорах





Мультиплексором называют комбинационное устройство, обеспечивающее передачу в желаемом порядке цифровой информации, поступающей по нескольким входам на один выход. Мультиплексоры обозначают через MUX, а также через MS.
Мультиплексоры и демультиплексоры
Мультиплексоры являются универсальными логическими устройствами, на основе которых создают различные комбинационные и последовательностные схемы. Мультиплексоры могут использовать в делителях частоты, триггерных устройствах, сдвигающих устройствах, для преобразования параллельного двоичного кода в последовательный и др.
Мультиплексоры (коммутаторы) являются селекторами каналов и служат для поочередного считывания информации с одного из n входов на общий выход в соответствии с адресным кодом.
Мультиплексор MUX (n – 1) имеет n = 2 m информационных входов (m – число адресных входов) и один выход.
Однонаправленные мультиплексоры выполнены на логических элементах и передают цифровую информацию с информационных входов на выход, двунаправленные – в обоих направлениях с помощью электронных ключей и называются селекторами-мультиплексорами (MS).
Эти логические элементы могут использоваться как демультиплексоры, а также для передачи сигналов произвольной формы.
Функционально мультиплексор можно изобразить в виде коммутатора, обеспечивающего подключение одного из нескольких входов (их называют информационными) к одному выходу устройства.
Кроме информационных входов в мультиплексоре имеются адресные входы и разрешающие (стробирующие). Сигналы на адресных входах определяют, какой конкретно информационный канал подключен к выходу.
Если между числом информационных входов n и числом адресных входов m действует соотношение n = 2m, то такой мультиплексор называют полным. Если n
| Таблица истинностимультиплексора MUX (2 – 1) | ||||
| № | Входы | Выход | ||
| Служебный | Информационные | Адресный | Информационный | |
| EI | X1 | X0 | A | F0 |
| – | – | – | ||
| – | X0 | X0 | ||
| X1 | – | X1 |
Примечание: вместо прочерка может использоваться любое значение переменной.
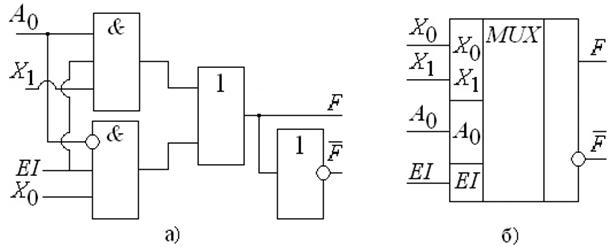
Схема мультиплексора MUX (2 – 1), рис. 3.1, разработана согласно таблице 3.1.
Часто мультиплексоры имеют дополнительный инверсный выход, что отражено в схеме.
Рис. Принципиальная схема: а – MUX (2 – 1), б – его условное обозначение
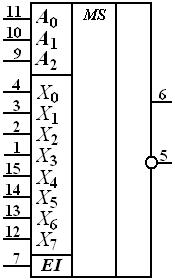
Пример. Характеристики и обозначение микросхемы К155КП7.
Это селектор — мультиплексор MS(8-1), соединяющий прямой и инверсный выходы с одним из восьми входов в соответствии с кодом адреса на трех адресных входах.
Имеется также служебный вход EI для разрешения работы мультиплексора в определенный интервал времени при условии EI =1 (стробирование).
Микросхема выполнена в пластмассовом корпусе 238.16-2 с двухрядным вертикальным расположением выводов.
Электрические параметры микросхемы К155КП7 приведены в табл.3.2, условное графическое обозначение на рис.3.2, назначение выводов в таблице истинности 3.3.

| Uпит., ном., В | |
| U 0 вых., не более, В | 0.4 |
| U 1 вых., не менее, В | 2.4 |
| I 0 вх., не более, мА | -1.6 |
| I 1 вх., не более, мА | 0.04 |
| t 1. 0 зд.р., не более, нс | |
| t 0. 1 зд.р., не более, нс | |
| Рпот., не более, мВт |
Рис. Обозначение микросхемы К155КП7
Таблица истинности селектора-мультиплексора К155КП7
| № | Входы | Выходы | |||||||||||
| Служебные | Информационные | Адресные | |||||||||||
| EI | X7 | X6 | X5 | X4 | X3 | X2 | X1 | X0 | A2 | A1 | A0 | F | /F |
| – | – | – | – | – | – | – | – | – | – | – | |||
| – | – | – | – | – | – | – | X0 | X0 | /X0 | ||||
| – | – | – | – | – | – | X1 | – | X1 | /X1 | ||||
| – | – | – | – | – | X2 | – | – | X2 | /X2 | ||||
| – | – | – | – | X3 | – | – | – | X3 | /X3 | ||||
| – | – | – | X4 | – | – | – | – | X4 | /X4 | ||||
| – | – | X5 | – | – | – | – | – | X5 | /X5 | ||||
| – | X6 | – | – | – | – | – | – | X6 | /X6 | ||||
| X7 | – | – | – | – | – | – | – | X7 | /X7 |
Примечание: значком «/» обозначается инверсия. Вместо прочерка может использоваться любое значение переменной.
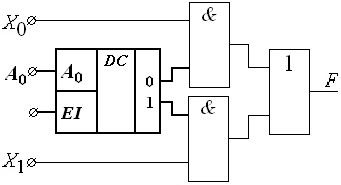
В состав мультиплексора обычно включают двоичный дешифратор, как, в качестве примера, показано на рис. 3.3 для простейшей схемы MUX (2-1).
Это позволяет управлять переключением информационных входов при помощи двоичных кодов, подаваемых на управляющие входы.
Количество информационных входов в таких схемах выбирают кратным степени числа два.
Таблица истинности Таблица 3.4
| Входы | Выход | |||
| EI | A0 | X1 | X0 | F |
| – | – | – | ||
| – | X0 | X0 | ||
| X1 | – | X1 |
а – на дешифраторе и логических элементах, управляемый двоичным кодом, б – его таблица истинности
Реализация логического выражения с помощью комбинационной логики может осуществляться на мультиплексорах.
Пример. Логическое выражение задано таблицей истинности (табл. 3.5), где A1, A0 аргументы функции F; X0, X1, X2, X3 – значения функции F для соответствующих значений аргументов A1, A0.
Аналогично можно получить постоянное запоминающее устройство.
При подаче на информационные входы фиксированных данных, их считывание с выхода F осуществляется с помощью адресных входов.
Таблица истинности устройства Таблица 3.5
| № | Входы | Выходы | |||||
| Служебные | Информационные | Адресные | |||||
| EI | X3 | X2 | X1 | X0 | A1 | A0 | F |
| – | – | – | – | – | – | ||
| – | – | – | |||||
| – | – | – | |||||
| – | – | – | |||||
| – | – | – |
Согласно таблице истинности подключены входы мультиплексора MUX(4-1), изображенного на рис. 3.4 , а, на рис. 3.4, б – аналогичная схема на механическом переключателе (вход EI не используется).
Рис. 3.4 Подключение мультиплексора: а – микросхема, б – механический аналог на переключателе для реализации логической функции
Схему можно упростить, если принять во внимание, что на наборах 2, 3 (табл. 3.5): A1 = 0, а значение функции F = 0. В тоже время, на наборах 4, 5: A1 = 1, а значение функции F = A0 и повторяет значения младшего разряда кодаX0.
Следовательно, таблицу 3.5 можно упростить (табл. 3.6), для наборов 2, 3 выбрать константу 0, для 4, 5 – значение X0, адресный вход установить A1.
Таблица истинности устройства
| № | Входы | Выходы | ||
| Служебные | Информационные | Адресные | ||
| EI | X1 | X0 | A0 | F |
| – | – | – | ||
| X0 | ||||
| X0 |
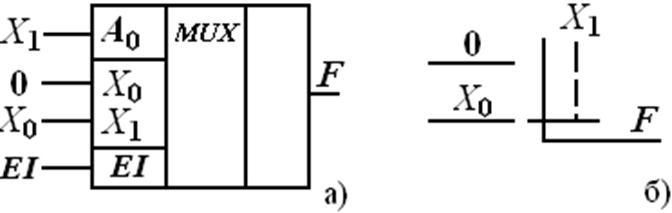
Рис. 3.5 Подключение мультиплексора: а – микросхема, б – механический аналог на переключателе для реализации логической функции
Схему также можно упростить, т.к. наборы 2, 3 (табл. 3.5) можно объединить, подав на А0: A1 = 0, при этом F = X0 = 0 (константа 0); на наборах 4, 5: A1 = 1, а значение функции F повторяет значения A0, которое подается на X1 (табл. 3.7, рис. 3.6).
Таблица истинности устройства
| № | Входы | Выходы | ||
| Служебные | Информационные | Адресные | ||
| EI | X1 | X0 | A1 | F |
| – | – | – | ||
| 2 | ||||
| – | A0 |
На основании табл. разработано устройство на MUX(2-1):
Рис. 3.6 Подключение мультиплексора:
б – механический аналог на переключателе для реализации логической функции
Источник
Составление таблицы истинности для мультиплексора
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Составление таблицы истинности
Нужно составить таблицу истинности для выражение: (А и В) или С путём написания программы с.
Программа для таблицы истинности
Привет всем! Я сделал программу для реализации таблицы истинности, но у меня возникает одна.
Таблицы истинности для формул
Построить таблицы истинности для формул:

Уважаемы знатоки! Помогите пожалуйста не знаю как реализовать в паскале таблицу истинности для.
Сообщение от DeadZone
Извините, может вопрос совсем глупый, т.к у меня этот предмет впервые.
Мы подаем, предположим А0 — 0 , А1 — 0, и подаем на DI0, DI1, DI2, DI3 — тоже 0 или 1?
Эта тема была перенесена из раздела Электротехника, ТОЭ.
Сообщение от DeadZone
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Формула для составления таблицы истинности
Не могу составить формулу, по которой бы заполнялся StringGrid нулями и единицами. Знаю, что число.
Составить таблицы истинности для функций
помогите плиз решить задания 1. Составить таблицы истинности для функций и построить.
Построить таблицы истинности для выражений
кто может посдсчитать: Построить таблицы истинности для выражений: A*B*C, все буквы с модулем.

Есть примерная формулировка задачи(Придумала её сама), В квартире усыновлено 3 светильника (F1.
Нужно построить таблицы истинности для выражений
Спасите, please. На носу уже аттестация и срочно нужно сдать контрольную (2 марта в 22:00), а.
Источник